Prove that if chords of congruent circles subtend equal angles at their centres,

Solution:

Let us consider two congruent circles (circles of same radius) with centres as O and O'.



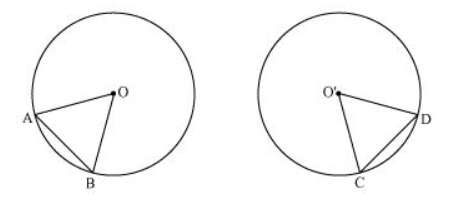
In $\triangle \mathrm{AOB}$ and $\triangle C O^{\prime} D$,

$\angle \mathrm{AOB}=\angle \mathrm{CO}^{\prime} \mathrm{D}($ Given $)$

$O A=O^{\prime} C$ (Radii of congruent circles)

$O B=O^{\prime} D$ (Radii of congruent circles)

$\therefore \triangle \mathrm{AOB} \cong \triangle \mathrm{CO}^{\prime} \mathrm{D}(\mathrm{SAS}$ congruence rule $)$

$\Rightarrow A B=C D(B y C P C T)$

Hence, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.