Prove that in a triangle, if the square of one side is equal

Given: if square of one side is equal to the sum of the squares of the other two sides, then we have to prove that the angle opposite the first side is a right angle.

Here, we are given a triangle ABC with. We need to prove that

.

Now, we construct a triangle PQR right angled at Q such that  and .

We have the following diagram.

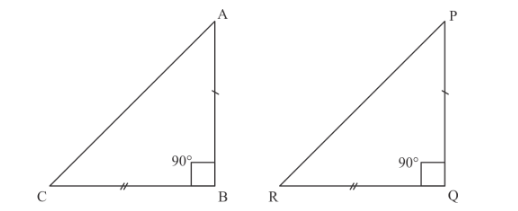
Now, in $\triangle \mathrm{PQR}$, we have

$\mathrm{PR}^{2}=\mathrm{PQ}^{2}+\mathrm{QR}^{2}$

$\Rightarrow \mathrm{PR}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}$…… (1)

But, it is given that

$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2} \ldots \ldots(2)$

From equations (1) and (2), we get

     $\mathrm{AC}^{2}=\mathrm{PR}^{2}$

$\Rightarrow \mathrm{AC}=\mathrm{PR} \ldots \ldots(3)$

From the above analysis in and, we have

$\mathrm{AB}=\mathrm{PQ}$

$\mathrm{BC}=\mathrm{QR}$

$\mathrm{AC}=\mathrm{PR}$

$\Rightarrow \Delta \mathrm{ABC}-\Delta \mathrm{PQR}$

$\Rightarrow \angle B=\angle Q$

Since $\angle Q=90^{\circ}$, therefore $\angle B=90^{\circ}$

Hence, $\angle \mathrm{B}=90^{\circ}$