Prove that in an equilateral triangle,

Let $A B C$ be an equilateral triangle and let $A D \perp B C$.

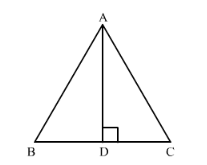
In $\triangle A D B$ and $\triangle A D C$ we have

$A B=A C$

$\angle B=\angle C$

And $\angle A D B=\angle A D C$

$\Rightarrow \triangle A D B \cong \triangle A D C$

So, $B D=D C$

$\Rightarrow B D=D C=\frac{1}{2} B C$

Since $\triangle A D B$ is a right triangle right-angled at $D .$ So

$A B^{2}=A D^{2}+B D^{2}$

$A B^{2}=A D^{2}+\left(\frac{1}{2} B C\right)^{2}$

$A B^{2}=A D^{2}+\frac{B C^{2}}{4}$

$A B^{2}=A D^{2}+\frac{A B^{2}}{4}$

$\frac{3}{4} A B^{2}=A D^{2}$

$3 A B^{2}=4 A D^{2}$

Hence proved.