Prove that the area of the equilateral triangle

Let a right triangle BAC in which ∠A is right angle and AC = y, AB = x.

Three equilateral triangles ΔAEC, Δ AFB and ΔCBD are drawn on the three sides of ΔABC. Again let area of triangles made on AC, AS and BC

are A1, A2 and A3, respectively.

To prove A3 = A1 + A2

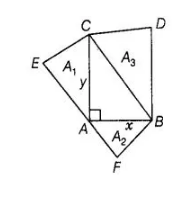
Proof $\ln \Delta C A B$, by Pythagoras theorem,

$B C^{2}=A C^{2}+A B^{2}$

$\Rightarrow \quad B C^{2}=y^{2}+x^{2}$

$\Rightarrow \quad B C=\sqrt{y^{2}+x^{2}}$

We know that, area of an equilateral triangle $=\frac{\sqrt{3}}{4}(\text { Side })^{2}$

$\therefore$ Area of equilateral $\triangle A E C, A_{1}=\frac{\sqrt{3}}{4}(A C)^{2}$

$\Rightarrow \quad A_{1}=\frac{\sqrt{3}}{4} y^{2}$ .....(i)

and area of equilateral $\triangle A F B, A_{2}=\frac{\sqrt{3}}{4}(A B)^{2}=\frac{\sqrt{3}}{4} \sqrt{\left(y^{2}+x^{2}\right)}$

$=\frac{\sqrt{3}}{4}\left(y^{2}+x^{2}\right)=\frac{\sqrt{3}}{4} y^{2}+\frac{\sqrt{3}}{4} x^{2}$

$=A_{1}+A_{2}$ [from Eqs. (i) and (ii)]

Hence proved.