Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
Given Two tangents PQ and PR are drawn from an external point P to a circle with centre 0.
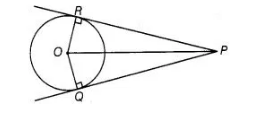
To prove Centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In ∠RPQ.
Construction Join $\mathrm{OR}$, and $\mathrm{OQ}$.
In $\triangle \mathrm{POP}$ and $\triangle \mathrm{POO}$
$\angle P R O=\angle P Q O=90^{\circ}$
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
$O R=O Q$ [radii of some circle]
Since OP is common
$\therefore \quad \triangle P R O \cong \triangle P Q O \quad$ [RHS]
Hence, $\angle R P O=\angle Q P O$ [by CPCT]
Thus, $O$ lies on angle bisecter of $P R$ and $P Q$.
Hence proved.