Prove that the line joining the mid-points

Given Let ABCD be a trapezium in which AB|| DC and let M and N be the mid-points of the diagonals AC and BD, respectively.

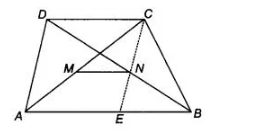
To prove $M N\|A B\| C D$

Construction Join $C N$ and produce it to meet $A B$ at $E$.

In $\triangle C D N$ and $\triangle E B N$, we have

$D N=B N$ [since, $N$ is the mid-point of $B D$ ]

and $\angle D C N=\angle B E N$ [alternate interior angles]

$\begin{array}{ll}\text { and } & \angle C D N=\angle E B N \quad \text { [alternate interior angles] }\end{array}$

$\therefore$ $D C=E B$ and $C N=N E$ [by CPCT rule]

Thus, in $\triangle C A E$, the points $M$ and $N$ are the mid-points of $A C$ and $C E$, respectively.

$\therefore \quad M N \| A E \quad$ [by mid-point theorem]

$\Rightarrow$ $M N\|A B\| C D$ Hence proved.