Prove that the line joining the points of contact of two parallel tangents of a circle passes through its centre

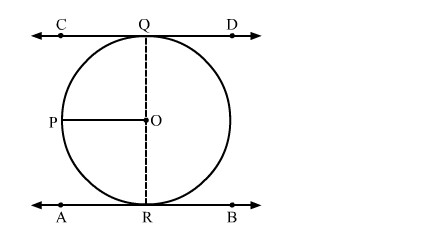
Suppose CD and AB are two parallel tangents of a circle with centre O
Construction: Draw a line parallel to CD passing through O i.e, OP
We know that the radius and tangent are perperpendular at their point of contact.
∠OQC = ∠ORA = 90∘
Now, ∠OQC + ∠POQ = 180∘       (co-interior angles)
⇒ ∠POQ = 180∘ − 90∘ = 90∘
Similarly, Now, ∠ORA + ∠POR = 180∘       (co-interior angles)
⇒ ∠POR = 180∘ − 90∘ = 90∘
Now, ∠POR + ∠POQ = 90∘ + 90∘ = 180∘
Since, ∠POR and ∠POQ are linear pair angles whose sum is 180∘
Hence, QR is a straight line passing through centre O.