Prove that the medians of an equilateral triangle are equal.

To prove the medians of an equilateral triangle are equal.

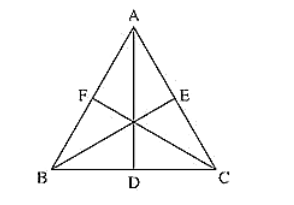
Median: The line Joining the vertex and midpoint of opposite side.  Now, consider an equilateral triangle ABC.

Let D, E, F are midpoints of BC, CA and AB.

Then, AD, BE and CF are medians of ABC.

Now,

D Is midpoint of BC ⟹ BD = DC = BC/2

Similarly, CE = EA = AC/2

AF = FB = AB/2

Since ΔABC is an equilateral triangle

⟹ AB = BC = CA  ... (i)

⟹ BD = DC = CE = EA = AF = FB = BC/2 = AC/2 = AB/2 .... (ii)

And also, ∠ABC = ∠BCA = ∠CAB = 60° ... (iii)

Now, consider ΔABD and ΔBCE AB = BC  [From (i)]

BD = CE  [From (ii)]

Now, in ΔTSR and ΔTRQ

TS = TR    [From (iii)]

∠ABD = ∠BCE            [From (iii)] [∠ABD and ∠ABC and ∠BCE and ∠BCA are same]

So, from SAS congruence criterion, we have

ΔABD = ΔBCE

AD = BE   .... (iv)

[Corresponding parts of congruent triangles are equal]

Now, consider ΔBCE and ΔCAF, BC = CA                         [From (i)]

∠BCE = ∠CAF             [From (ii)]

[∠BCE and ∠BCA and  ∠CAF and ∠CAB are same]

CE = AF                [From (ii)]

So, from SAS congruence criterion, we have

ΔBCE = ΔCAF

BE = CF (v)

[Corresponding parts of congruent triangles are equal]

From (iv) and (v), we have

AD = BE = CF

Median AD = Median BE = Median CF

The medians of an equilateral triangle are equal.

Hence proved