Question:
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
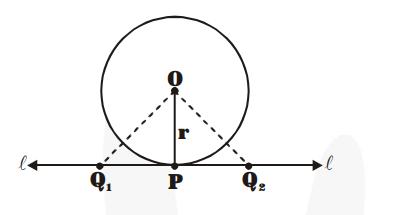
In figure, line $\ell$ is tangent to the circle at $\mathrm{P} . \mathrm{O}$ is the centre of the circle.
OP = radius of the circle.
If we have some points $Q_{1}, Q_{2}$, etc. on $\ell$, then we find that $O P$ is the shortest distance from $\mathrm{O}$ in comparison to the distances $\mathrm{OQ}_{1}, \mathrm{OQ}_{2}$, etc.
Therefore, $\mathrm{OP} \perp \ell .$ Hence, the perpendicular OP drawn to the tangent line at P passes through the centre O of the circle.
