Prove that the quadrilateral formed

Solution:

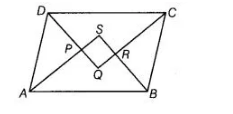
Given Let ABCD be a parallelogram and AP, BR, CR, be are the bisectors of ∠A, ∠B, ∠C and ∠D, respectively.

To prove Quadrilateral PQRS is a rectangle.

Proof Since, ABCD is a parallelogram, then DC || AB and DA is a transversal.

∠A+∠D= 180°

[sum of cointerior angles of a parallelogram is 180°]

=> ½ ∠A+  ½ ∠D = 90° [dividing both sides by 2]

∠PAD + ∠PDA = 90°

∠APD = 90°    [since,sum of all angles of a triangle is 180°]

∴ ∠SPQ = 90°     [vertically opposite angles]

 

∠PQR = 90°

∠QRS = 90°

and ∠PSR = 90°

Thus, PQRS is a quadrilateral whose each angle is 90°.

Hence, PQRS is a rectangle.