Prove that the semi-vertical angle

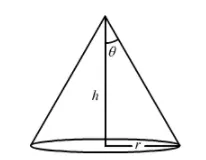
Let:

Radius of the base $=r$,

Height $=h$,

Slant height $=1$,

Volume $=V$,

Curved surface area $=C$

As, Volume, $V=\frac{1}{3} \pi r^{2} h$

$\Rightarrow h=\frac{3 V}{\pi r^{2}}$

Also, the slant height, $l=\sqrt{h^{2}+r^{2}}$

$=\sqrt{\left(\frac{3 V}{\pi r^{2}}\right)^{2}+r^{2}}$

$=\sqrt{\frac{9 V^{2}}{\pi^{2} r^{4}}+r^{2}}$

$=\sqrt{\frac{9 V^{2}+\pi^{2} r^{6}}{\pi^{2} r^{4}}}$

$\Rightarrow l=\frac{\sqrt{9 V^{2}+\pi^{2} r^{6}}}{\pi r^{2}}$

Now,

$\mathrm{CSA}, C=\pi r l$

$\Rightarrow C(r)=\pi r \frac{\sqrt{9 V^{2}+\pi^{2} r^{6}}}{\pi r^{2}}$

$\Rightarrow C(r)=\frac{\sqrt{9 V^{2}+\pi^{2} r^{6}}}{r}$

$\Rightarrow C^{\prime}(r)=\frac{r \times \frac{6 \mathrm{x}^{2} r^{6}}{2 \sqrt{9 V^{2}+\mathrm{x}^{2,6}}}-\sqrt{9 V^{2}+\pi^{2} r^{6}}}{r^{2}}$

$=\frac{\left[\frac{3 \pi^{2} r^{6}-\left(g V^{2}+\pi^{2} r^{6}\right)}{\sqrt{9 V^{2}+x^{2} r^{6}}}\right]}{r^{2}}$

$=\frac{3 \pi^{2} r^{6}-9 V^{2}-\pi^{2} r^{6}}{r^{2} \sqrt{9 V^{2}+\pi^{2} r^{6}}}$

$=\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{9 V^{2}+\pi^{2} r^{6}}}$

For maxima or minima, $C^{\prime}(r)=0$

$\Rightarrow \frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{9 V^{2}+\pi^{2} r^{6}}}=0$

$\Rightarrow 2 \pi^{2} r^{6}-9 V^{2}=0$

$\Rightarrow 2 \pi^{2} r^{6}=9 V^{2}$

$\Rightarrow V^{2}=\frac{2 \pi^{2} r^{6}}{9}$

$\Rightarrow V=\sqrt{\frac{2 \pi^{2} r^{6}}{9}}$

$\Rightarrow V=\frac{\pi r^{3} \sqrt{2}}{3}$ or $r=\left(\frac{3 V}{\pi \sqrt{2}}\right)^{\frac{1}{3}}$

So, $h=\frac{3}{\pi r^{2}} \times \frac{\pi r^{3} \sqrt{2}}{3}$

$\Rightarrow h=r \sqrt{2}$

$\Rightarrow \frac{h}{r}=\sqrt{2}$

$\Rightarrow \cot \theta=\sqrt{2}$

$\therefore \theta=\cot ^{-1}(\sqrt{2})$

Also,

Since, for $r<\left(\frac{3 V}{\pi \sqrt{2}}\right)^{\frac{1}{3}}, C^{\prime}(r)<0$ and for $r>\left(\frac{3 V}{\pi \sqrt{2}}\right)^{\frac{1}{3}}, C^{\prime}(r)>0$

So, the curved surface for $r=\left(\frac{3 V}{\pi \sqrt{2}}\right)^{\frac{1}{3}}$ or $V=\frac{\pi r^{3} \sqrt{2}}{3}$ is the least.