Prove that the surface area of a sphere is equal

We have the following figure to visualize the situation

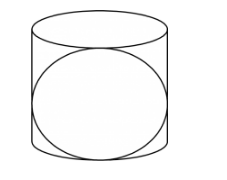
Let the radius of the sphere is r. Therefore, the surface area of the sphere is

$S=4 \pi \times r^{2}$

$=4 \pi r^{2}$

The circumscribed cylinder of the sphere must have radius r cm and height 2r cm. Therefore, the curved surface area of the cylinder is

$S_{1}=2 \pi r \times 2 r$

$=4 \pi r^{2}$

Hence, S and S1 are same. Thus the proof is complete.