If bisectors of $\angle A$ and $\angle B$ of a quadrilateral $A B C D$ intersect each other at $P$, of $\angle B$ and $\angle C$ at $Q$, of $\angle C$ and $\angle D$ at $R$ and of $\angle D$ and $\angle A$ at $S$, then $P Q R S$ is a
(a) rectangle
(b) rhombus
(c) parallelogram
(d) quadrilateral whose opposite angles are supplementary
(d) Given, $A B C D$ is a quadrilateral and all angles bisectors form a quadrilateral $P Q R S$.
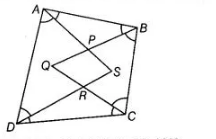
We know that, sum of all angles in a quadrilateral is $360^{\circ}$.
$\therefore \quad \angle A+\angle B+\angle C+\angle D=360^{\circ}$
On dividing both sides by 2 , we get
$\frac{1}{2}(\angle A+\angle B+\angle C+\angle D)=\frac{360^{\circ}}{2}$
$\Rightarrow \quad \angle P A B+\angle P B A+\angle R C D+\angle R D C=180^{\circ}$ $\ldots(i)$
[since, $A P$ and $P B$ are the bisectors of $\angle A$ and $\angle B$ respectively also $R C$ and $R D$ are the bisectors of $\angle C$ and $\angle D$ respectively]
Now, in $\triangle A P B$,
$\angle P A B+\angle A B P+\angle B P A=180^{\circ}$
[by angle sum property of a triangle]
$\Rightarrow \quad \angle P A B+\angle A B P=180^{\circ}-\angle B P A \quad$... (ii)
Similarly in $\triangle R D C$,
$\angle R D C+\angle D C R+\angle C R D=180^{\circ}$
[by angle sum property of a triangle]
$\Rightarrow \quad \angle R D C+\angle D C R=180^{\circ}-\angle C R D \quad \ldots$ (ii)
On substituting the value Egs. (ii) and (iii) in Eg. (i), we get
$180^{\circ}-\angle B P A+180^{\circ}-\angle D R C=180^{\circ}$
$\Rightarrow \quad \angle B P A+\angle D R C=180^{\circ}$
$\Rightarrow \quad \angle S P Q+\angle S R Q=180^{\circ}$
$[\because \angle B P A=\angle S P Q$ and $\angle D R C=\angle S R Q$ vertically opposite angles $]$
Hence, $P Q R S$ is a quadrilateral whose opposite angles are supplementary.
