If $P\left(\frac{1}{2}, 4\right)$ is the mid-point of the line segment joining the points $Q(-6,5)$ and $f(-2,3)$, then the value of a is
(a)-4
(b) -12
(c) 12
(d) -6
(b) Given that, $P\left(\frac{1}{2}, 4\right)$ is the mid-point of the line segment joining the points $Q(-6,5)$ and $R(-2,3)$, which shows in the figure
given below
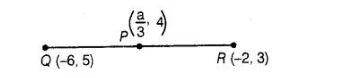
$\therefore$ Mid-point of $Q R=P\left(\frac{-6-2}{2}, \frac{5+3}{2}\right)=P(-4,4)$
$\left[\right.$ since, mid-point of line segment having points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$$\left.=\left(\frac{\left(x_{1}+x_{2}\right)}{2}, \frac{\left(y_{1}+y_{2}\right)}{2}\right)\right]$
But mid-point $P\left(\frac{a}{3}, 4\right)$ is given.
$\therefore$ $\left(\frac{a}{3}, 4\right)=(-4,4)$
On comparing the coordinates, we get
$\frac{a}{3}=-4$
$\therefore$ $a=-12$
Hence, the required value of a is -12.