Question:
Let $A_{1}, A_{2}, A_{3}, \ldots \ldots$ be squares such that for each $n \geq 1$, the length of the side of $A_{n}$ equals the length of diagonal of $\mathrm{A}_{n+1}$. If the length of $\mathrm{A}_{1}$ is $12 \mathrm{~cm}$, then the smallest value of $\mathrm{n}$ for which area of $\mathrm{A}_{n}$ is less than one, is
Solution:
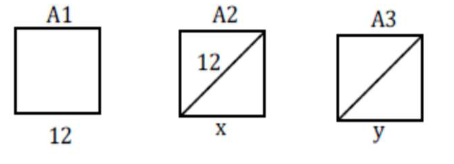
$x=\frac{12}{\sqrt{2}} \quad y=\frac{12}{(\sqrt{2})^{2}}$
$\therefore$ Side lengths are in G.P.
$\mathrm{T}_{\mathrm{n}}=\frac{12}{(\sqrt{2})^{\mathrm{n}-1}}$'
$\therefore \quad$ Area $=\frac{144}{2^{n-1}}<1 \quad \Rightarrow 2^{n-1}>144$
Smallest $\mathrm{n}=9$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
