Prove the result that the velocity $v$ of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height $h$ is given by $v^{2}=\frac{2 g h}{\left(1+k^{2} / R^{2}\right)}$.
Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
A body rolling on an inclined plane of height h,is shown in the following figure:
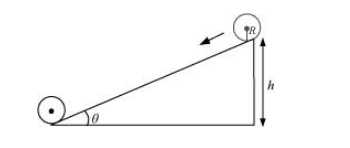
m = Mass of the body
R = Radius of the body
K = Radius of gyration of the body
v = Translational velocity of the body
h =Height of the inclined plane
g = Acceleration due to gravity
Total energy at the top of the plane, $E_{1}=m g h$
Total energy at the bottom of the plane, $E_{\mathrm{b}}=\mathrm{KE}_{\mathrm{rot}}+\mathrm{KE}_{\mathrm{trans}}$
$=\frac{1}{2} I \omega^{2}+\frac{1}{2} m v^{2}$
But $I=m k^{2}$ and $\omega=\frac{v}{R}$
$\therefore E_{\mathrm{b}}=\frac{1}{2}\left(m k^{2}\right)\left(\frac{v^{2}}{R^{2}}\right)+\frac{1}{2} m v^{2}$
$=\frac{1}{2} m v^{2} \frac{k^{2}}{R^{2}}+\frac{1}{2} m v^{2}$
$=\frac{1}{2} m v^{2}\left(1+\frac{k^{2}}{R^{2}}\right)$
From the law of conservation of energy, we have
$E_{\mathrm{T}}=E_{\mathrm{b}}$
$m g h=\frac{1}{2} m v^{2}\left(1+\frac{k^{2}}{R^{2}}\right)$
$\therefore v=\frac{2 \mathrm{~g} h}{\left(1+k^{2} / R^{2}\right)}$
Hence, the given result is proved.