Reaction between N2 and O2 takes place as follows:
$2 \mathrm{~N}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g}) \longleftrightarrow 2 \mathrm{~N}_{2} \mathrm{O}(\mathrm{g})$
If a mixture of $0.482 \mathrm{~mol}$ of $\mathrm{N}_{2}$ and $0.933 \mathrm{~mol}$ of $\mathrm{O}_{2}$ is placed in a $10 \mathrm{~L}$ reaction vessel and allowed to form $\mathrm{N}_{2} \mathrm{O}$ at a temperature for which $K_{c}=2.0 \times 10^{-37}$, determine the composition of equilibrium mixture.
Let the concentration of $\mathrm{N}_{2} \mathrm{O}$ at equilibrium be $x$.
The given reaction is:
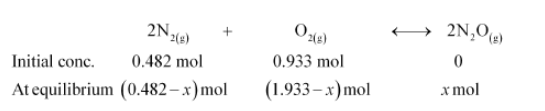
Therefore, at equilibrium, in the 10 L vessel:
$\left[\mathrm{N}_{2}\right]=\frac{0.482-x}{10},\left[\mathrm{O}_{2}\right]=\frac{0.933-x / 2}{10},\left[\mathrm{~N}_{2} \mathrm{O}\right]=\frac{x}{10}$
The value of equilibrium constant i.e., $K_{\mathrm{c}}=2.0 \times 10^{-37}$ is very small. Therefore, the amount of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$ reacted is also very small. Thus, $x$ can be neglected from the expressions of molar concentrations of $\mathrm{N}_{2}$ and $\mathrm{O}_{2}$.
Then,
$\left[\mathrm{N}_{2}\right]=\frac{0.482}{10}=0.0482 \mathrm{~mol} \mathrm{~L}^{-1}$ and $\left[\mathrm{O}_{2}\right]=\frac{0.933}{10}=0.0933 \mathrm{~mol} \mathrm{~L}^{-1}$
Now,
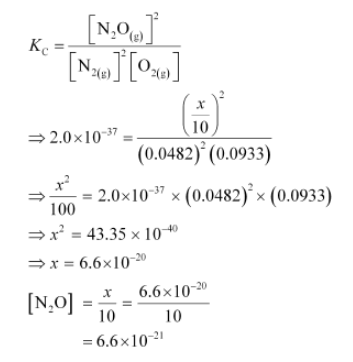
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
