Question.
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres
Solution:
A circle is a collection of points which are equidistant from a fixed point. This fixed point is called as the centre of the circle and this equal distance is called as radius of the circle. And thus, the shape of a circle depends on its radius. Therefore, it can be observed that if we try to superimpose two circles of equal radius, then both circles will cover each other. Therefore, two circles are congruent if they have equal radius.
Consider two congruent circles having centre O and O' and two chords AB and CD of equal lengths.
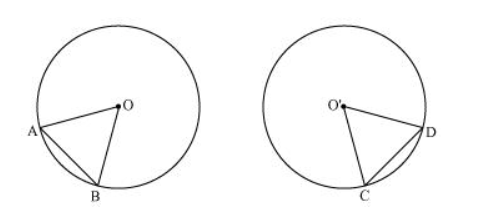
In $\triangle A O B$ and $\triangle C O^{\prime} D$,
$A B=C D$ (Chords of same length)
OA $=O^{\prime} C$ (Radii of congruent circles)
$O B=O^{\prime} D$ (Radii of congruent circles)
$\therefore \triangle \mathrm{AOB} \cong \triangle \mathrm{CO}^{\prime} \mathrm{D}(\mathrm{SSS}$ congruence rule $)$
$\Rightarrow \angle A O B=\angle C O^{\prime} D(B y C P C T)$
Hence, equal chords of congruent circles subtend equal angles at their centres.
Consider two congruent circles having centre O and O' and two chords AB and CD of equal lengths.

In $\triangle A O B$ and $\triangle C O^{\prime} D$,
$A B=C D$ (Chords of same length)
OA $=O^{\prime} C$ (Radii of congruent circles)
$O B=O^{\prime} D$ (Radii of congruent circles)
$\therefore \triangle \mathrm{AOB} \cong \triangle \mathrm{CO}^{\prime} \mathrm{D}(\mathrm{SSS}$ congruence rule $)$
$\Rightarrow \angle A O B=\angle C O^{\prime} D(B y C P C T)$
Hence, equal chords of congruent circles subtend equal angles at their centres.
