Question:
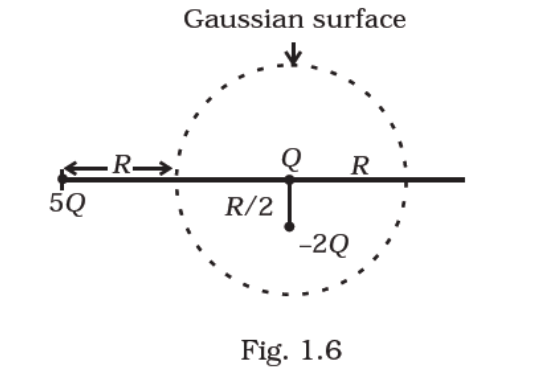
Refer to the arrangement of charges in Fig. 1.6 and a Gaussian surface of radius R with Q at the centre. Then
(a) total flux through the surface of the sphere is ‒Q/εo
(b) field on the surface of the sphere is ‒Q/(4πεoR2)
(c) flux through the surface of sphere due to 5Q is zero
(d) field on the surface of sphere due to –2Q is same everywhere
Solution:
Gauss' law states that total electric flux of an enclosed surface is given by q/εo. Here, q is the net charge enclosed by the Gaussian surface.
From the figure,
Net charge inside the surface is = Q ‒ 2Q = ‒ Q.
Net flux through the surface of the sphere = ‒ Q/εo
Here, charge 5Q lies outside the Gaussian surface, so it will not make no contribution to electric flux through the given surface.
