Represent

Solution:

We are asked to represent $\sqrt{6}, \sqrt{7}$ and $\sqrt{8}$ on the number line

We will follow certain algorithm to represent these numbers on real line

We will consider point A as reference point to measure the distance

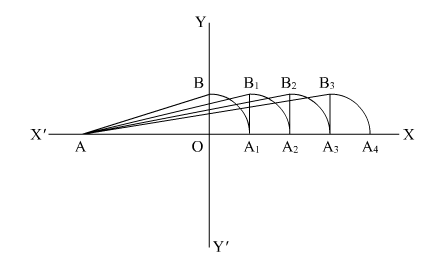
(1) First of all draw a line AX and YY’ perpendicular to AX

(2) Consider $A O=2$ unit and $O B=1$ unit, so

$A B=\sqrt{2^{2}+1^{2}}$

$=\sqrt{5}$

(3) Take A as center and AB as radius, draw an arc which cuts line AX at A1

(4) Draw a perpendicular line A1B1 to AX such that  and 

(5) Take A as center and AB1 as radius and draw an arc which cuts the line AX at A2.

 

Here 

$A B_{1}=A A_{2}$

$=\sqrt{A A_{1}{ }^{2}+A_{1} B_{1}{ }^{2}}$

$=\sqrt{(\sqrt{5})^{2}+1}$

$=\sqrt{6}$ unit

So $A A_{2}=\sqrt{6}$ unit

So $A_{2}$ is the representation for $\sqrt{6}$

(1) Draw line A2B2 perpendicular to AX

 

(2) Take A center and AB2 as radius and draw an arc which cuts the horizontal line at A3 such that 

$A B_{2}=A A_{3}$

$=\sqrt{A A_{2}^{2}+A_{2} B_{2}^{2}}$

$=\sqrt{(\sqrt{6})^{2}+1}$

$=\sqrt{7}$ unit

So point $A 3$ is the representation of $\sqrt{7}$

(3) Again draw the perpendicular line $A_{3} B_{3}$ to $A X$

(4) Take $A$ as center and $A B 3$ as radius and draw an arc which cuts the horizontal line at $A 4$

Here;

$A B_{3}=A A_{4}$

$=\sqrt{A A_{3}^{2}+A_{3} B_{3}^{2}}$

$=\sqrt{(\sqrt{7})^{2}+1^{2}}$

$=\sqrt{8}$ unit

$A 4$ is basically the representation of $\sqrt{8}$