Represent

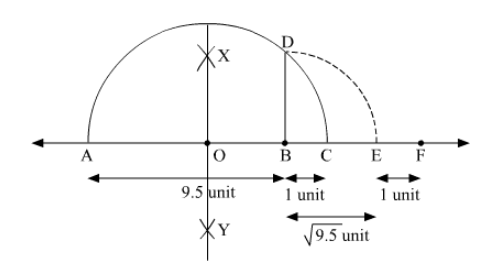
To represent $(1+\sqrt{9.5})$ on the number line, follow the following steps of construction:

(i) Mark two points A and B on a given line such that AB = 9.5 units.

(ii) From B, mark a point C on the same given line such that BC = 1 unit.

(iii) Find the mid point of AC and mark it as O.

(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.

(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.

(vi)  With B as centre and radius BD, draw an arc intersecting the given line at point E.

(vii) From E, mark a point F on the same given line such that EF = 1 unit.

Thus, let us treat the given line as the number line, with $\mathrm{B}$ as $0, \mathrm{C}$ as $1, \mathrm{E}$ as $\sqrt{9.5}$ and so on, then point $\mathrm{F}$ represents $(1+\sqrt{9.5})$.

Justification:

Here, in semi-circle, radii $\mathrm{OA}=\mathrm{OC}=\mathrm{OD}=\frac{9.5+1}{2}=\frac{10.5}{2}=5.25$ units

And, $\mathrm{OB}=\mathrm{AB}-\mathrm{AO}=9.5-5.25=4.25$ units

In a right angled triangle $\mathrm{OBD}$,

$\mathrm{BD}=\sqrt{\mathrm{OD}^{2}-\mathrm{OB}^{2}}$

$=\sqrt{5.25^{2}-4.25^{2}}$

$=\sqrt{(5.25+4.25)(5.25-4.25)} \quad\left[a^{2}-b^{2}=(a+b)(a-b)\right]$

$=\sqrt{9.5 \times 1}$

$=\sqrt{9.5}$

So, $\mathrm{BF}=\mathrm{BE}+\mathrm{EF}=\sqrt{9.5}+1 \quad[\mathrm{BD}=\mathrm{BE}=\sqrt{9.5}($ Radii $)]$