Roohi travels 300 km to her home partly by train and partly by bus.

Solution:

Let the speed of the train be x km/hour that of the bus be y km/hr, we have the following cases

Case I: When Roohi travels 300 Km by train and the rest by bus

Time taken by Roohi to travel $60 \mathrm{Km}$ by train $=\frac{60}{x} h r s$

Time taken by Roohi to travel $(300-60)=240 \mathrm{Km}$ by bus $=\frac{240}{y} h r s$

Total time taken by Roohi to cover $300 \mathrm{Km}=\frac{60}{x}+\frac{240}{y}$

It is given that total time taken in 4 hours

$\frac{60}{x}+\frac{240}{y}=4$

$60\left(\frac{1}{x}+\frac{4}{y}\right)=4$

$\left(\frac{1}{x}+\frac{4}{y}\right)=\frac{4}{60}$

$\frac{1}{x}+\frac{4}{y}=\frac{1}{15} \cdots(i)$

Case II: When Roohi travels 100 km by train and the rest by bus

Time taken by Roohi to travel $100 \mathrm{Km}$ by train $=\frac{100}{x} h r s$

Time taken by Roohi to travel $(300-100)=200 \mathrm{Km}$ by bus $=\frac{200}{y} h r s$

In this case total time of the journey is 4 hours 10 minutes

$\frac{100}{x}+\frac{200}{y}=4 h r s 10 \mathrm{~min}$ utes

$\frac{100}{x}+\frac{200}{y}=4 \frac{10}{60}$

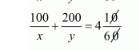
$\frac{100}{x}+\frac{200}{y}=\frac{25}{6}$

$100\left(\frac{1}{x}+\frac{2}{y}\right)=\frac{25}{6}$

$\frac{1}{x}+\frac{2}{y}=\frac{25}{6} \times \frac{1}{100}$

$\frac{1}{x}+\frac{2}{y}=\frac{1}{24}$$\ldots$ (i)

Putting $\frac{1}{x}=u$ and $\frac{1}{y}=u$, the equations $(i)$ and $(i i)$ reduces to

$1 u+4 v=\frac{1}{15} \cdots(i i i)$

$1 u+2 v=\frac{1}{24} \cdots(i v)$

Subtracting equation (iv) from (iii)we get

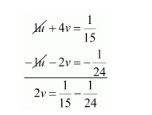
$2 v=\frac{24-15}{360}$

$2 v=\frac{9}{360}$

$2 v=\frac{9}{360}$

$v=\frac{1}{40} \times \frac{1}{2}$

$v=\frac{1}{80}$

Putting $v=\frac{1}{80}$ in equation (iii), we get

$1 u+4 v=\frac{1}{15}$

$1 u+4 \times \frac{1}{80}=\frac{1}{15}$

$1 u+\frac{4}{80}=\frac{1}{15}$

$1 u=\frac{1}{15}-\frac{4}{80}$

$1 u=\frac{1}{15}-\frac{1}{20}$

$1 u=\frac{20-15}{300}$

$1 u=\frac{5}{300}$

$u=\frac{1}{60}$

Now

$u=\frac{1}{60}$

$\frac{1}{x}=\frac{1}{60}$

$x=60$

and

$v=\frac{1}{80}$

$\frac{1}{y}=\frac{1}{80}$

$y=80$

Hence, the speed of the train is $60 \mathrm{~km} / \mathrm{hr}$,

The speed of the bus is $80 \mathrm{~km} / \mathrm{hr}$