Ship $A$ is sailing towards north-east with velocity $\vec{v}=30 \hat{i}+50 \hat{j} \mathrm{~km} / \mathrm{hr}$ where $\hat{i}$ points east and $\hat{j}$, north.
Ship B is at a distance of $80 \mathrm{~km}$ east and $150 \mathrm{~km}$ north of Ship A and is sailing towards west at $10 \mathrm{~km} / \mathrm{hr}$. A will be at minimum distance from $B$ in:
Correct Option: , 2
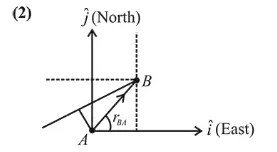
$\vec{v}_{A}=30 \hat{i}+50 \hat{j} \mathrm{~km} / \mathrm{hr}$
$\vec{v}_{B}=(-10 \hat{i}) \mathrm{km} / \mathrm{hr}$
$r_{B A}=(80 \hat{i}+150 \hat{j}) \mathrm{km}$
$\vec{v}_{B A}=\vec{v}_{B}-\vec{v}_{A}=-10 \hat{i}-30 \hat{i}-50 \hat{i}$
$=40 \hat{i}-50 \hat{j}$
$t_{\text {minimum }}=\frac{\left|\left(\vec{r}_{B A}\right) \cdot\left(\vec{v}_{B A}\right)\right|}{\left|\left(\vec{v}_{B A}\right)\right|^{2}}$
$=\frac{|(80 \hat{i}+150 \hat{j})(-40 \hat{i}-50 \hat{j})|}{(10 \sqrt{41})^{2}}$
$\therefore t=\frac{10700}{10 \sqrt{41} \times 10 \sqrt{41}}=\frac{107}{41}=2.6 \mathrm{hrs}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.