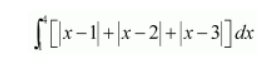
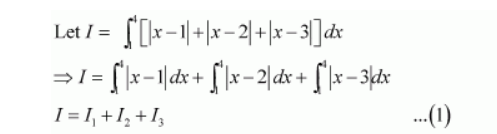
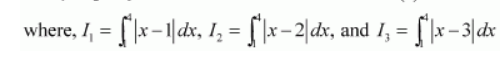
$I_{1}=\int_{1}^{4}|x-1| d x$
$(x-1) \geq 0$ for $1 \leq x \leq 4$
$\therefore I_{1}=\int_{1}^{4}(x-1) d x$
$\Rightarrow I_{1}=\left[\frac{x^{2}}{x}-x\right]_{1}^{4}$
$\Rightarrow I_{1}=\left[8-4-\frac{1}{2}+1\right]=\frac{9}{2}$ ...(2)
$I_{2}=\int_{1}^{4}|x-2| d x$
$x-2 \geq 0$ for $2 \leq x \leq 4$ and $x-2 \leq 0$ for $1 \leq x \leq 2$
$\therefore I_{2}=\int_{1}^{2}(2-x) d x+\int_{2}^{4}(x-2) d x$
$\Rightarrow I_{2}=\left[2 x-\frac{x^{2}}{2}\right]_{1}^{2}+\left[\frac{x^{2}}{2}-2 x\right]_{2}^{4}$
$\Rightarrow I_{2}=\left[4-2-2+\frac{1}{2}\right]+[8-8-2+4]$
$\Rightarrow I_{2}=\frac{1}{2}+2=\frac{5}{2}$ (3)
$I_{3}=\int_{1}^{4}|x-3| d x$
$x-3 \geq 0$ for $3 \leq x \leq 4$ and $x-3 \leq 0$ for $1 \leq x \leq 3$
$\therefore I_{3}=\int_{1}^{3}(3-x) d x+\int_{3}^{4}(x-3) d x$
$\Rightarrow I_{3}=\left[3 x-\frac{x^{2}}{2}\right]_{1}^{3}+\left[\frac{x^{2}}{2}-3 x\right]_{3}^{4}$
$\Rightarrow I_{3}=\left[9-\frac{9}{2}-3+\frac{1}{2}\right]+\left[8-12-\frac{9}{2}+9\right]$
$\Rightarrow I_{3}=[6-4]+\left[\frac{1}{2}\right]=\frac{5}{2}$ ...(4)
From equations (1), (2), (3), and (4), we obtain
$I=\frac{9}{2}+\frac{5}{2}+\frac{5}{2}=\frac{19}{2}$
