Show that

Let $I=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}} d x$

$\Rightarrow I=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x+\cos x)}{\sqrt{-(-\sin 2 x)}} d x$

$\Rightarrow I=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin x+\cos x}{\sqrt{-(-1+1-2 \sin x \cos x)}} d x$

$\Rightarrow I=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x+\cos x)}{\sqrt{1-\left(\sin ^{2} x+\cos ^{2} x-2 \sin x \cos x\right)}} d x$

$\Rightarrow I=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x+\cos x) d x}{\sqrt{1-(\sin x-\cos x)^{2}}}$

Let $(\sin x-\cos x)=t \Rightarrow(\sin x+\cos x) d x=d t$

When $x=\frac{\pi}{6}, t=\left(\frac{1-\sqrt{3}}{2}\right)$ and when $x=\frac{\pi}{3}, t=\left(\frac{\sqrt{3}-1}{2}\right)$

$I=\int_{\frac{1-\sqrt{3}}{2}}^{\sqrt{3}-1} \frac{d t}{\sqrt{1-t^{2}}}$

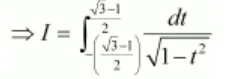
As $\frac{1}{\sqrt{1-(-t)^{2}}}=\frac{1}{\sqrt{1-t^{2}}}$, therefore, $\frac{1}{\sqrt{1-t^{2}}}$ is an even function.

It is known that if $f(x)$ is an even function, then $\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x$

$\begin{aligned} \Rightarrow I &=2 \int_{0}^{\frac{\sqrt{3}-1}{2}} \frac{d t}{\sqrt{1-t^{2}}} \\ &=\left[2 \sin ^{-1} t\right]_{0}^{\frac{\sqrt{3}-1}{2}} \\ &=2 \sin ^{-1}\left(\frac{\sqrt{3}-1}{2}\right) \end{aligned}$