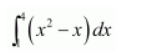
Let $I=\int_{1}^{4}\left(x^{2}-x\right) d x$
$=\int_{1}^{4} x^{2} d x-\int_{1}^{4} x d x$
Let $I=I_{1}-I_{2}$, where $I_{1}=\int_{1}^{4} x^{2} d x$ and $I_{2}=\int_{1}^{4} x d x$ ...(1)
It is known that,
$\int_{a}^{b} f(x) d x=(b-a) \lim _{n \rightarrow \infty} \frac{1}{n}[f(a)+f(a+h)+f(a+(n-1) h)]$, where $h=\frac{b-a}{n}$
For $I_{1}=\int_{1}^{4} x^{2} d x$
$a=1, b=4$, and $f(x)=x^{2}$
$\therefore h=\frac{4-1}{n}=\frac{3}{n}$
$I_{1}=\int_{1}^{4} x^{2} d x=(4-1) \lim _{n \rightarrow \infty} \frac{1}{n}[f(1)+f(1+h)+\ldots+f(1+(n-1) h)]$
$=3 \lim \frac{1}{1}\left[1^{2}+\left(1+\frac{3}{1}\right)^{2}+\left(1+2 \cdot \frac{3}{2}\right)^{2}+\ldots\left(1+\frac{(n-1) 3}{4}\right)^{2}\right]$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[1^{2}+\left\{1^{2}+\left(\frac{3}{n}\right)^{2}+2 \cdot \frac{3}{n}\right\}+\ldots+\left\{1^{2}+\left(\frac{(n-1) 3}{n}\right)^{2}+\frac{2 \cdot(n-1) \cdot 3}{n}\right\}\right]$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[\left(1^{2}+\ldots+1^{2}\right)+\left(\frac{3}{n}\right)^{2}\left\{1^{2}+2^{2}+\ldots+(n-1)^{2}\right\}+2 \cdot \frac{3}{n}\{1+2+\ldots+(n-1)\}\right]$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[n+\frac{9}{n^{2}}\left\{\frac{(n-1)(n)(2 n-1)}{6}\right\}+\frac{6}{n}\left\{\frac{(n-1)(n)}{2}\right\}\right]$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[n+\frac{9 n}{6}\left(1-\frac{1}{n}\right)\left(2-\frac{1}{n}\right)+\frac{6 n-6}{2}\right]$
$=3 \lim _{n \rightarrow \infty}\left[1+\frac{9}{6}\left(1-\frac{1}{n}\right)\left(2-\frac{1}{n}\right)+3-\frac{3}{n}\right]$
$=3[1+3+3]$
$=3[7]$
$I_{1}=21$ ...(2)
For $I_{2}=\int_{1}^{4} x d x$,
$a=1, b=4$, and $f(x)=x$
$\Rightarrow h=\frac{4-1}{n}=\frac{3}{n}$
$\begin{aligned} \therefore I_{2} &=(4-1) \lim _{n \rightarrow \infty} \frac{1}{n}[f(1)+f(1+h)+\ldots f(a+(n-1) h)] \\ &=3 \lim _{n \rightarrow \infty} \frac{1}{n}[1+(1+h)+\ldots+(1+(n-1) h)] \\ &=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[1+\left(1+\frac{3}{n}\right)+\ldots+\left\{1+(n-1) \frac{3}{n}\right\}\right] \\ &=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[(1+1+\ldots+1)+\frac{3}{n}(1+2+\ldots+(n-1))\right] \end{aligned}$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[n+\frac{3}{n}\left\{\frac{(n-1) n}{2}\right\}\right]$
$=3 \lim _{n \rightarrow \infty} \frac{1}{n}\left[1+\frac{3}{2}\left(1-\frac{1}{n}\right)\right]$
$=3\left[1+\frac{3}{2}\right]$
$=3\left[\frac{5}{2}\right]$
$I_{2}=\frac{15}{2}$ ...(3)
From equations (2) and (3), we obtain
$I=I_{1}+I_{2}=21-\frac{15}{2}=\frac{27}{2}$