Show that

$y d x+\left(x-y^{2}\right) d y=0$

$\Rightarrow y d x=\left(y^{2}-x\right) d y$

$\Rightarrow \frac{d x}{d y}=\frac{y^{2}-x}{y}=y-\frac{x}{y}$

$\Rightarrow \frac{d x}{d y}+\frac{x}{y}=y$

This is a linear differential equation of the form:

$\frac{d y}{d x}+p x=Q$ ( where $p=\frac{1}{y}$ and $Q=y$ )

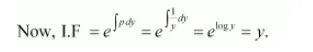
The general solution of the given differential equation is given by the relation,

$x(\mathrm{I} . \mathrm{F} .)=\int(\mathrm{Q} \times \mathrm{I} . \mathrm{F} .) d y+\mathrm{C}$

$\Rightarrow x y=\int(y \cdot y) d y+\mathrm{C}$

$\Rightarrow x y=\int y^{2} d y+\mathrm{C}$

$\Rightarrow x y=\frac{y^{3}}{3}+\mathrm{C}$

$\Rightarrow x=\frac{y^{2}}{3}+\frac{\mathrm{C}}{y}$