Show that any positive odd integers is of the form

Here we have to prove that for any positive integer q, the positive odd integer will be form of 4q+1 or 4q+3.

Now let us suppose that the positive odd integer is a then by Euclid’s division rule

a = 4q + r ……(1 )

Where q (quotient) and r (remainder) are positive integers, and 

We are putting the values of r from 0 to 3 in equation (1), we get

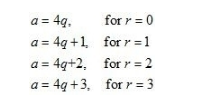
But we can easily see that 4q and 4q+2 are both even numbers.

Therefore for any positive value q, the positive odd integer will be the form of 4q+1 and 4q+3.