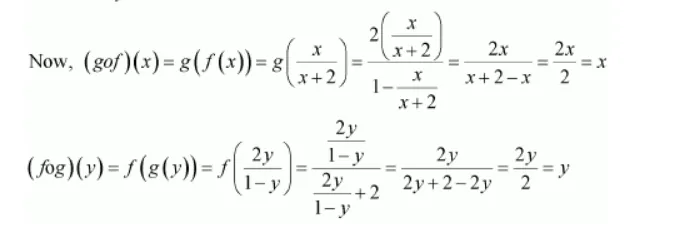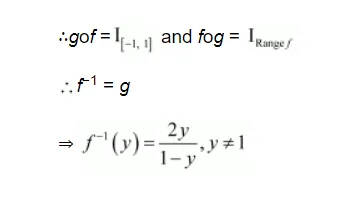Show that $f:[-1,1] \rightarrow \mathbf{R}$, given by $f(x)=\frac{x}{(x+2)}$ is one-one. Find the inverse of the function $f:[-1,1] \rightarrow$ Range $f$.
(Hint: For $y \in$ Range $f, y=f(x)=\frac{x}{x+2}$, for some $x$ in $[-1,1]$, i.e., $x=\frac{2 y}{(1-y)}$ )
$f:[-1,1] \rightarrow \mathrm{R}$ is given as $f(x)=\frac{x}{(x+2)}$.
Let $f(x)=f(y)$.
$\Rightarrow \frac{x}{x+2}=\frac{y}{y+2}$
$\Rightarrow x y+2 x=x y+2 y$
$\Rightarrow 2 x=2 y$
$\Rightarrow x=y$
∴ f is a one-one function.
It is clear that $f:[-1,1] \rightarrow$ Range $f$ is onto.
$\therefore f:[-1,1] \rightarrow$ Range $f$ is one-one and onto and therefore, the inverse of the function:
$f:[-1,1] \rightarrow$ Range $f$ exists.
Let $g$ : Range $f \rightarrow[-1,1]$ be the inverse of $f$.
Let y be an arbitrary element of range f.
Since $f:[-1,1] \rightarrow$ Range $f$ is onto, we have:
$y=f(x)$ for same $x \in[-1,1]$
$\Rightarrow y=\frac{x}{x+2}$
$\Rightarrow x y+2 y=x$
$\Rightarrow x(1-y)=2 y$
$\Rightarrow x=\frac{2 y}{1-y}, y \neq 1$
Now, let us define $g$ : Range $f \rightarrow[-1,1]$ as
$g(y)=\frac{2 y}{1-y}, y \neq 1$