Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical

Solution:

The given right circular cone of fixed height (h) and semi-vertical angle (α) can be drawn as:

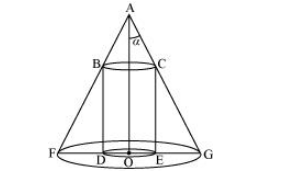
Here, a cylinder of radius R and height H is inscribed in the cone.

Then, $\angle \mathrm{GAO}=\alpha, \mathrm{OG}=r, \mathrm{OA}=h, \mathrm{OE}=R$, and $\mathrm{CE}=H$.

We have,

r = h tan α

Now, since ΔAOG is similar to ΔCEG, we have:

$\frac{\mathrm{AO}}{\mathrm{OG}}=\frac{\mathrm{CE}}{\mathrm{EG}}$

$\Rightarrow \frac{h}{r}=\frac{H}{r-R} \quad[\mathrm{EG}=\mathrm{OG}-\mathrm{OE}]$

$\Rightarrow H=\frac{h}{r}(r-R)=\frac{h}{h \tan \alpha}(h \tan \alpha-R)=\frac{1}{\tan \alpha}(h \tan \alpha-R)$

Now, the volume (V) of the cylinder is given by,

$\mathrm{V}=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

Now, $\frac{d V}{d R}=0$

$\mathrm{V}=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

Now,$\frac{d V}{d R}=0$

$\Rightarrow 2 \pi R h=\frac{3 \pi R^{2}}{\tan \alpha}$

$\Rightarrow 2 h \tan \alpha=3 R$

$\Rightarrow R=\frac{2 h}{3} \tan \alpha$

Now, $\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi R}{\tan \alpha}$

And, for $R=\frac{2 h}{3} \tan \alpha$, we have:

$\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi}{\tan \alpha}\left(\frac{2 h}{3} \tan \alpha\right)=2 \pi h-4 \pi h=-2 \pi h<0$

∴By second derivative test, the volume of the cylinder is the greatest when

$R=\frac{2 h}{3} \tan \alpha .$

When $R=\frac{2 h}{3} \tan \alpha, H=\frac{1}{\tan \alpha}\left(h \tan \alpha-\frac{2 h}{3} \tan \alpha\right)=\frac{1}{\tan \alpha}\left(\frac{h \tan \alpha}{3}\right)=\frac{h}{3}$.

Thus, the height of the cylinder is one-third the height of the cone when the volume of the cylinder is the greatest.

Now, the maximum volume of the cylinder can be obtained as:

$\pi\left(\frac{2 h}{3} \tan \alpha\right)^{2}\left(\frac{h}{3}\right)=\pi\left(\frac{4 h^{2}}{9} \tan ^{2} \alpha\right)\left(\frac{h}{3}\right)=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$

Hence, the given result is proved.