Show that in a right angled triangle, the hypotenuse is the longest side.

Solution:



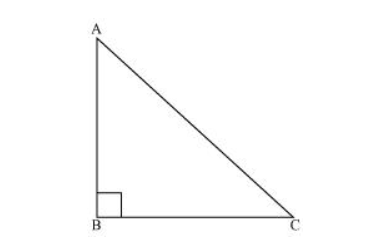
Let us consider a right-angled triangle $\mathrm{ABC}$, right-angled at $\mathrm{B}$.

In $\triangle \mathrm{ABC}$

$\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}$ (Angle sum property of a triangle)

$\angle \mathrm{A}+90^{\circ}+\angle \mathrm{C}=180^{\circ}$

$\angle \mathrm{A}+\angle \mathrm{C}=90^{\circ}$

Hence, the other two angles have to be acute (i.e., less than $90^{\circ}$ ).

$\therefore \angle B$ is the largest angle in $\triangle A B C$.

$\Rightarrow \angle B>\angle A$ and $\angle B>\angle C$

$\Rightarrow \mathrm{AC}>\mathrm{BC}$ and $\mathrm{AC}>\mathrm{AB}$

[In any triangle, the side opposite to the larger (greater) angle is longer.]

Therefore, $A C$ is the largest side in $\triangle A B C$.

However, $A C$ is the hypotenuse of $\triangle A B C$. Therefore, hypotenuse is the longest side in a right-angled triangle.