Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Solution:



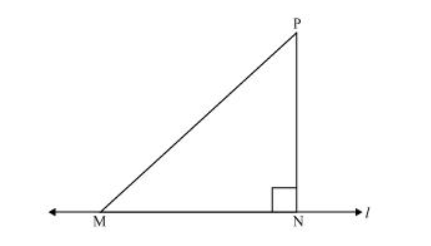
Let us take a line l and from point P (i.e., not on line l), draw two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.

In $\triangle P N M$,

$\angle \mathrm{N}=90^{\circ}$

$\angle \mathrm{P}+\angle \mathrm{N}+\angle \mathrm{M}=180^{\circ}$ (Angle sum property of a triangle)

$\angle P+\angle M=90^{\circ}$

Clearly, $\angle M$ is an acute angle.

$\therefore \angle \mathrm{M}<\angle \mathrm{N}$

$\Rightarrow$ PN < PM (Side opposite to the smaller angle is smaller)

Similarly, by drawing different line segments from $\mathrm{P}$ to $\mathrm{l}$, it can be proved that $\mathrm{PN}$ is smaller in comparison to them.

Therefore, it can be observed that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.