Show that of all the rectangles inscribed in a given fixed circle,

Let a rectangle of length l and breadth b be inscribed in the given circle of radius a.

Then, the diagonal passes through the centre and is of length 2a cm.

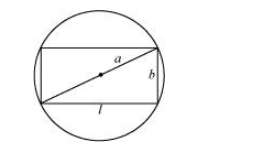
Now, by applying the Pythagoras theorem, we have:

$(2 a)^{2}=l^{2}+b^{2}$

$\Rightarrow b^{2}=4 a^{2}-l^{2}$

$\Rightarrow b=\sqrt{4 a^{2}-l^{2}}$

$\therefore$ Area of the rectangle, $A=I \sqrt{4 a^{2}-l^{2}}$

$\therefore \frac{d A}{d l}=\sqrt{4 a^{2}-l^{2}}+l \frac{1}{2 \sqrt{4 a^{2}-l^{2}}}(-2 l)=\sqrt{4 a^{2}-l^{2}}-\frac{l^{2}}{\sqrt{4 a^{2}-l^{2}}}$

$=\frac{4 a^{2}-2 l^{2}}{\sqrt{4 a^{2}-I^{2}}}$

$\frac{d^{2} A}{d l^{2}}=\frac{\sqrt{4 a^{2}-l^{2}}(-4 l)-\left(4 a^{2}-2 l^{2}\right) \frac{(-2 l)}{2 \sqrt{4 a^{2}-l^{2}}}}{\left(4 a^{2}-l^{2}\right)}$

$=\frac{\left(4 a^{2}-l^{2}\right)(-4 l)+l\left(4 a^{2}-2 l^{2}\right)}{\left(4 a^{2}-l^{2}\right)^{\frac{3}{2}}}$

$=\frac{-12 a^{2} l+2 l^{3}}{\left(4 a^{2}-l^{2}\right)^{\frac{3}{2}}}=\frac{-2 l\left(6 a^{2}-l^{2}\right)}{\left(4 a^{2}-l^{2}\right)^{\frac{3}{2}}}$

Now, $\frac{d A}{d l}=0$ gives $4 a^{2}=2 l^{2} \Rightarrow l=\sqrt{2} a$

$\Rightarrow b=\sqrt{4 a^{2}-2 a^{2}}=\sqrt{2 a^{2}}=\sqrt{2} a$

Now, when $l=\sqrt{2} a$,

$\frac{d^{2} \mathrm{~A}}{d l^{2}}=\frac{-2(\sqrt{2} a)\left(6 a^{2}-2 a^{2}\right)}{2 \sqrt{2} a^{3}}=\frac{-8 \sqrt{2} a^{3}}{2 \sqrt{2} a^{3}}=-4<0$

$\therefore$ By the second derivative test, when $l=\sqrt{2} a$, then the area of the rectangle is the maximum.

Since $l=b=\sqrt{2} a$, the rectangle is a square.

Hence, it has been proved that of all the rectangles inscribed in the given fixed circle, the square has the maximum area.