Show that semi-vertical angle of right circular cone of given

Solution:

Let r be the radius, l be the slant height and h be the height of the cone of given surface area, S.

Also, let α be the semi-vertical angle of the cone.

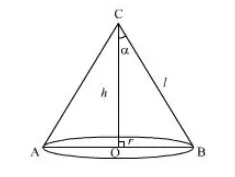
Then $S=\pi r l+\pi r^{2}$

$\Rightarrow l=\frac{S-\pi r^{2}}{\pi r} \ldots .(1)$ 

Let $V$ be the volume of the cone.

$\begin{aligned} \Rightarrow V^{2} &=\frac{1}{9} \pi^{2} r^{4} h^{2} \\ &=\frac{1}{9} \pi^{2} r^{4}\left(l^{2}-r^{2}\right)\left[\text { Asl }^{2}=r^{2}+h^{2}\right] \\ &=\frac{1}{9} \pi^{2} r^{4}\left[\left(\frac{S-\pi r^{2}}{\pi r}\right)^{2}-r^{2}\right] \\ &=\frac{1}{9} \pi^{2} r^{4}\left[\frac{\left(S-\pi r^{2}\right)^{2}-\pi^{2} r^{4}}{\pi^{2} r^{2}}\right] \\ &=\frac{1}{9} r^{2}\left(S^{2}-2 S \pi r^{2}\right) \\ \Rightarrow V^{2} &=\frac{1}{9} S r^{2}\left(S-2 \pi r^{2}\right) \ldots . .(2) \end{aligned}$

Differentiating (2) with respect to $r$, we get

$2 V \frac{d V}{d r}=\frac{1}{9} S\left(2 S r-8 \pi r^{3}\right)$

For maximum or minimum, put $\frac{d V}{d r}=0$

$\Rightarrow \frac{1}{9} S\left(2 S r-8 \pi r^{3}\right)=0$

$\Rightarrow 2 S r-8 \pi r^{3}=0 \quad($ As $S \neq 0)$

$\Rightarrow S=4 \pi r^{2} \quad($ As $r \neq 0)$

$\Rightarrow r^{2}=\frac{S}{4 \pi}$

Differentiating again with respect to r, we get

$\begin{aligned} 2 V \frac{d^{2} V}{d r^{2}}+2 &\left(\frac{d V}{d r}\right)^{2}=\frac{1}{9} S\left(2 S-24 \pi r^{2}\right) \\ \Rightarrow 2 V \frac{d^{2} V}{d r^{2}} &=\frac{1}{9} S\left(2 S-24 \pi \times \frac{S}{4 \pi}\right) \quad\left(\text { As } \frac{d V}{d r}=0 \text { and } r^{2}=\frac{S}{4 \pi}\right) \\ &=\frac{1}{9} S(2 S-6 S) \\ &=-\frac{4}{9} S^{2}<0 \end{aligned}$

Thus, $V$ is maximum when $\mathrm{S}=4 \pi r^{2}$

As $S=\pi r l+\pi r^{2}$

$\Rightarrow 4 \pi r^{2}=\pi r l+\pi r^{2}$

$\Rightarrow 3 \pi r^{2}=\pi r l$

$\Rightarrow l=3 r$

Now, in $\Delta \mathrm{COB}$,

$\begin{aligned} \operatorname{Sin} \alpha &=\frac{O B}{B C} \\ &=\frac{r}{l} \\ &=\frac{r}{3 r} \\ &=\frac{1}{3} \\ \Rightarrow \alpha &=\operatorname{Sin}^{-1}\left(\frac{1}{3}\right) \end{aligned}$