Show that the diagonals of a parallelogram divide it into four triangles of equal area.

Solution:



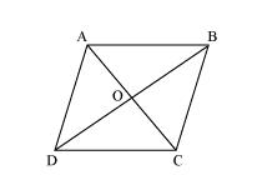
We know that diagonals of parallelogram bisect each other.

Therefore, O is the mid-point of AC and BD.

BO is the median in ΔABC. Therefore, it will divide it into two triangles of equal areas.

$\therefore$ Area $(\Delta \mathrm{AOB})=$ Area $(\Delta \mathrm{BOC}) \ldots(1)$

In $\triangle B C D, C O$ is the median.

$\therefore$ Area $(\Delta \mathrm{BOC})=$ Area $(\Delta \mathrm{COD}) \ldots(2)$

Similarly, Area $(\Delta \mathrm{COD})=$ Area $(\Delta \mathrm{AOD}) \ldots(3)$

From equations $(1),(2)$, and $(3)$, we obtain

Area $(\Delta \mathrm{AOB})=$ Area $(\Delta \mathrm{BOC})=$ Area $(\Delta \mathrm{COD})=$ Area $(\Delta \mathrm{AOD})$

Therefore, it is evident that the diagonals of a parallelogram divide it into four triangles of equal area.