Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.

Solution:



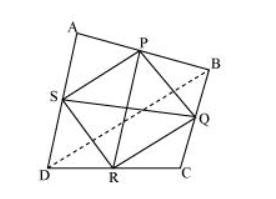
Let ABCD is a quadrilateral in which P, Q, R, and S are the mid-points of sides AB, BC, CD, and DA respectively. Join PQ, QR, RS, SP, and BD.

In ΔABD, S and P are the mid-points of AD and AB respectively. Therefore, by using mid-point theorem, it can be said that

$S P \| B D$ and $S P=\frac{1}{2} B D \ldots$(1)

Similarly in $\triangle B C D$,

$Q R \| B D$ and $Q R=\frac{1}{2} B D$..(2)

From equations (1) and (2), we obtain

$S P \| Q R$ and $S P=Q R$

In quadrilateral SPQR, one pair of opposite sides is equal and parallel to each other. Therefore, SPQR is a parallelogram.

We know that diagonals of a parallelogram bisect each other.

Hence, PR and QS bisect each other.