Show that the lines

Solution:

Given: $3 x-4 y+5=0$

$7 x-8 y+5=0$

and $4 x+5 y=45$

or $4 x+5 y-45=0$

To show: Given lines are concurrent

The lines $a_{1} x+b_{1} y+c_{1}=0, a_{1} x+b_{1} y+c_{1}=0$ and $a_{1} x+b_{1} y+c_{1}=0$ are concurrent if

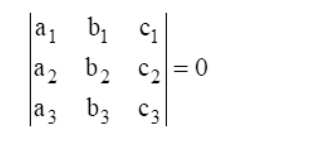
We know that,

We have,

$a_{1}=3, b_{1}=-4, c_{1}=5$

$a_{2}=7, b_{2}=-8, c_{2}=5$

$a_{3}=4, b_{2}=5, c_{3}=-45$

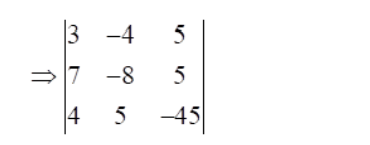
Now, expanding along first row, we get

$\Rightarrow 3[(-8)(-45)-(5)(5)]-(-4)[(7)(-45)-(4)(5)]+5[(7)(5)-(4)(-8)]$

$\Rightarrow 3[360-25]+4[-315-20]+5[35+32]$

$\Rightarrow 3[335]+4[-335]+5[67]$

$\Rightarrow 1005-1340+335$

$\Rightarrow 1340-1340$

= 0

So, the given lines are concurrent.

Now, we have to find the point of intersection of the given lines

$3 x-4 y+5=0$

$7 x-8 y+5=0$

and $4 x+5 y-45=0 \ldots(A)$

We know that, if three lines are concurrent the point of intersection of two lines lies on the third line.

So, firstly, we find the point of intersection of two lines

$3 x-4 y+5=0, \ldots$ (i)

$7 x-8 y+5=0 \ldots$ (ii)

Multiply the eq. (i) by 2, we get

$6 x-8 y+10=0$ .........(iii)

On subtracting eq. (iii) from (ii), we get

$7 x-8 y+5-6 x+8 y-10=0$

$\Rightarrow x-5=0$

$\Rightarrow x=5$

Putting the value of x in eq. (i), we get

$3(5)-4 y+5=0$

$\Rightarrow 15-4 y+5=0$

$\Rightarrow 20-4 y=0$

$\Rightarrow-4 y=-20$

$\Rightarrow y=5$

Thus, the first two lines intersect at the point (5, 5). Putting x = 5 and y = 5 in eq. (A), we get

$4(5)+5(5)-45$

$=20+25-45$

$=45-45$

$=0$

So, point $(5,5)$ lies on line $4 x+5 y-45=0$

Hence, the point of intersection is (5, 5)