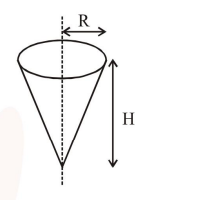
Shown in the figure is a hollow icecream cone (it is open at the top). If its mass is M, radius of its top, $\mathrm{R}$ and height, $\mathrm{H}$, then its moment of inertia about its axis is:
Correct Option: 1
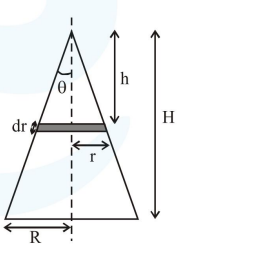
Area $=\pi R \ell=\pi R\left(\sqrt{\mathrm{H}^{2}+\mathrm{R}^{2}}\right)$
Area of element $\mathrm{d} \mathrm{A}=2 \pi \mathrm{rd} \ell==2 \pi \mathrm{r} \frac{\mathrm{dh}}{\cos \theta}$
mass of element $\mathrm{dm}=\frac{\mathrm{M}}{\pi \mathrm{R} \sqrt{\mathrm{H}^{2}+\mathrm{R}^{2}}} \times \frac{2 \pi \mathrm{rdh}}{\cos \theta}$
$\mathrm{dm}=\frac{2 \mathrm{Mh} \tan \theta \mathrm{dh}}{\mathrm{R} \sqrt{\mathrm{H}^{2}+\mathrm{R}^{2}} \cos \theta} \quad($ here $\mathrm{r}=\mathrm{h} \tan \theta)$
$\mathrm{I}=\int(\mathrm{dm}) \mathrm{r}^{2}=\int \frac{\mathrm{h}^{2} \tan ^{2} \theta}{\cos \theta}\left(\frac{2 \mathrm{~m}}{\mathrm{R}} \frac{\mathrm{h} \tan \theta}{\sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}}\right) \mathrm{dh}$
$=\frac{2 \mathrm{M}}{\cos \theta \mathrm{R}} \frac{\tan ^{3} \theta}{\sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}}$
$\int_{0}^{\mathrm{H}} \mathrm{h}^{3} \mathrm{dh}=\frac{\mathrm{MR}^{2} \mathrm{H}^{4}}{2 \mathrm{RH}^{3} \sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}} \cos \theta}$
$=\frac{\mathrm{MR}^{2} \mathrm{H} \sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}}{2 \sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}} \times \mathrm{H}}$
$=\frac{\mathrm{MR}^{2}}{2}$
