Simplify:

To simplify, we will proceed as follows:

(i) $(x-y)(x+y)\left(x^{2}+y^{2}\right)\left(x^{4}+y^{4}\right)$

$=\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)\left(x^{4}+y^{4}\right) \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=\left(x^{4}-y^{4}\right)\left(x^{4}+y^{4}\right) \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=x^{8}-x^{8} \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

(ii) $(2 x-1)(2 x+1)\left(4 x^{2}+1\right)\left(16 x^{4}+1\right)$

$=\left((2 x)^{2}-1^{2}\right)\left(4 x^{2}+1\right)\left(16 x^{4}+1\right) \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=\left(4 x^{2}-1\right)\left(4 x^{2}+1\right)\left(16 x^{4}+1\right)$

$=\left\{\left(4 x^{2}\right)^{2}-\left(1^{2}\right)^{2}\right\}\left(16 x^{4}+1\right) \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=\left(16 x^{4}-1\right) \quad\left(16 x^{4}+1\right)$

$=\left(16 x^{4}\right)^{2}-1^{2} \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=256 x^{8}-1$

(iii) $(7 m-8 n)^{2}+(7 m+8 n)^{2}$

$=2(7 m)^{2}+2(8 n)^{2} \quad\left[\because(a-b)^{2}+(a+b)^{2}=2 a^{2}+2 b^{2}\right]$

$=98 m^{2}+128 n^{2}$

(iv) $(2.5 p-1.5 q)^{2}-(1.5 p-2.5 q)^{2}$

$=(2.5 p)^{2}+(1.5 q)^{2}-2(2.5 p)(1.5 q)-\left[(1.5 p)^{2}+(2.5 q)^{2}-2(1.5 p)(2.5 q)\right]$

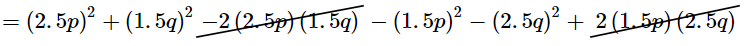
$=(2.5 p)^{2}-(1.5 p)^{2}+(1.5 q)^{2}-(2.5 q)^{2}$

$=[(2.5 p+1.5 p)(2.5 p-1.5 p)]+[(1.5 q+2.5)(1.5 q-2.5 q)] \quad\left[\because(a+b)(a-b)=a^{2}-b^{2}\right]$

$=4 p \times p+4 q \times(-q)$

$=4 p^{2}-4 q^{2}$

$=4\left(p^{2}-4 q^{2}\right)$

(v) $\left(m^{2}-n^{2} m\right)^{2}+2 m^{3} n^{2}$

$=\left(m^{2}\right)^{2}+\left(n^{2} m\right)^{2} \quad\left[\because(a-b)^{2}+2 a b=a^{2}+b^{2}\right]$

$=m^{4}+n^{4} m^{2}$