Simplify each of the following and express it in the form (a + ib):

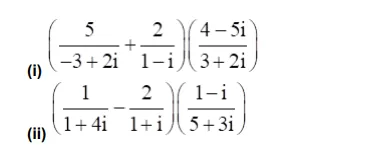
Given:

$\left(\frac{5}{-3+2 i}+\frac{2}{1-i}\right)\left(\frac{4-5 i}{3+2 i}\right)$

$=\left[\frac{5(1-i)+2(-3+2 i)}{(-3+2 i)(1-i)}\right]\left(\frac{4-5 i}{3+2 i}\right)$ [Taking the LCM]

$=\left[\frac{5-5 i-6+4 i}{(-3)(1-i)+2 i(1-i)}\right]\left(\frac{4-5 i}{3+2 i}\right)$

$=\left[\frac{-1-i}{-3+3 i+2 i-2 i^{2}}\right]\left(\frac{4-5 i}{3+2 i}\right)$

$=\left[\frac{-(1+i)}{-3+5 i-2(-1)}\right]\left(\frac{4-5 i}{3+2 i}\right)$

$=\left(\frac{-(1+i)}{-1+5 i}\right)\left(\frac{4-5 i}{3+2 i}\right)$

$=\frac{-1(4-5 i)-i(4-5 i)}{-1(3+2 i)+5 i(3+2 i)}$

$=\frac{-4+5 i-4 i+5 i^{2}}{-3-2 i+15 i+10 i^{2}}$

$=\frac{-4+i+5(-1)}{-3+13 i+10(-1)}\left[\right.$ Putting $\left.i^{2}=-1\right]$

$=\frac{-9+i}{-13+13 i}$

$=\frac{-(9-i)}{-(13-13 i)}$

$=\frac{9-i}{13-13 i}$

Now, rationalizing by multiply and divide by the conjugate of $(13-13 \mathrm{i})$

$=\frac{9-i}{13-13 i} \times \frac{13+13 i}{13+13 i}$

$=\frac{(9-i)(13+13 i)}{(13-13 i)(13+13 i)}$

$=\frac{117+117 i-13 i-13 i^{2}}{(13)^{2}-(13 i)^{2}}\left[\because(a-b)(a+b)=\left(a^{2}-b^{2}\right)\right]$

$=\frac{117+104 i-13(-1)}{169-169 i^{2}}\left[\because \dot{\mathrm{i}}^{2}=-1\right]$

$=\frac{130+104 i}{169\left(1-i^{2}\right)}$

$=\frac{13(10+8 i)}{169[1-(-1)]}$ [Taking 13 common]

$=\frac{10+8 i}{13 \times 2}$

$=\frac{5+4 i}{13}$

$=\frac{5}{13}+\frac{4}{13} i$

(ii) Given:

$\left(\frac{1}{1+4 i}-\frac{2}{1+i}\right)\left(\frac{1-i}{5+3 i}\right)$

$=\left[\frac{1(1+i)-2(1+4 i)}{(1+4 i)(1+i)}\right]\left(\frac{1-i}{5+3 i}\right)$ [Taking the LCM]

$=\left[\frac{1+i-2-8 i}{(1)(1+i)+4 i(1+i)}\right]\left(\frac{1-i}{5+3 i}\right)$

$=\left[\frac{-1-7 i}{1+i+4 i+4 i^{2}}\right]\left(\frac{1-i}{5+3 i}\right)$

$=\left[\frac{-1-7 i}{1+5 i+4(-1)}\right]\left(\frac{1-i}{5+3 i}\right)$

$=\left(\frac{-1-7 i}{-3+5 i}\right)\left(\frac{1-i}{5+3 i}\right)$

$=\left(\frac{-1-7 i}{-3+5 i}\right)\left(\frac{1-i}{5+3 i}\right)$

$=\frac{-1(1-i)-7 i(1-i)}{-3(5+3 i)+5 i(5+3 i)}$

$=\frac{-1+i-7 i+7 i^{2}}{-15-9 i+25 i+15 i^{2}}$

$=\frac{-1-6 i+7(-1)}{-15+16 i+15(-1)}$

$=\frac{-6 i-8}{16 i-30}$

$=\frac{-2(4+3 i)}{-2(15-8 i)}$

$=\frac{4+3 i}{15-8 i}$

Now, rationalizing by multiply and divide by the conjugate of $(15+8 \mathrm{i})$

$=\frac{4+3 i}{15-8 i} \times \frac{15+8 i}{15+8 i}$

$=\frac{(4+3 i)(15+8 i)}{(15)^{2}-(8 i)^{2}}\left[\because(a-b)(a+b)=\left(a^{2}-b^{2}\right)\right]$

$=\frac{4(15+8 i)+3 i(15+8 i)}{225-64 i^{2}}$

$=\frac{60+32 i+45 i+24 i^{2}}{225-64(-1)}\left[\because i^{2}=-1\right]$

$=\frac{60+77 i+24(-1)}{225+64}$

$=\frac{36+77 i}{289}$

$=\frac{36}{289}+\frac{77}{289} i$