Size of agricultural holdings in a survey of 200

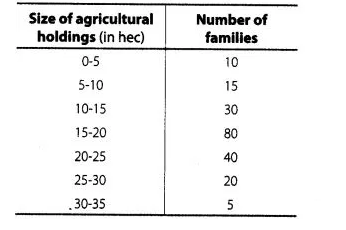
(i) Here, $N=200$

Now, $\frac{N}{2}=\frac{200}{2}=100$, which lies in the interval 15-20.

Lower limit, $l=15, h=5, f=80$ and $c f=55$

$\therefore \quad$ Median $=l+\left(\frac{\frac{N}{2}-c f}{f}\right) \times h=15+\left(\frac{100-55}{80}\right) \times 5$

$=15+\left(\frac{45}{16}\right)=15+2.81=17.81 \mathrm{hec}$

(ii) In a given table 80 is the highest frequency.

So, the modal class is $15-20$.

Here, $l=15, f_{m}=80, f_{1}=30, f_{2}=40$ and $h=5$

$\therefore$ Mode $=l+\left(\frac{f_{m}-f_{1}}{2 f_{m}-f_{1}-f_{2}}\right) \times h$

$=15+\left(\frac{80-30}{2 \times 80-30-40}\right) \times 5$

$=15+\left(\frac{50}{160-70}\right) \times 5$

$=15+\left(\frac{50}{90}\right) \times 5=15+\frac{25}{9}$

$=15+2.77=17.77$ hec