Question:
Sketch the graph of $y=|x+3|$ and evaluate $\int_{-6}^{0}|x+3| d x$
Solution:
The given equation is $y=|x+3|$
The corresponding values of x and y are given in the following table.
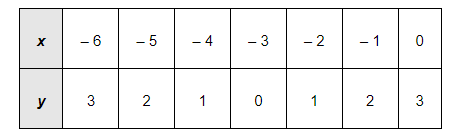
On plotting these points, we obtain the graph of $y=|x+3|$ as follows.
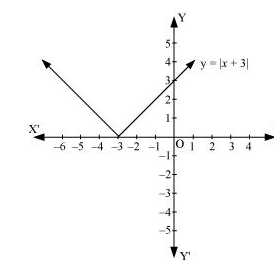
It is known that, $(x+3) \leq 0$ for $-6 \leq x \leq-3$ and $(x+3) \geq 0$ for $-3 \leq x \leq 0$
$\therefore \int_{-6}^{0}|(x+3)| d x=-\int_{-6}^{-3}(x+3) d x+\int_{-3}^{0}(x+3) d x$
$=-\left[\frac{x^{2}}{2}+3 x\right]_{-6}^{-3}+\left[\frac{x^{2}}{2}+3 x\right]_{-3}^{0}$
$=-\left[\left(\frac{(-3)^{2}}{2}+3(-3)\right)-\left(\frac{(-6)^{2}}{2}+3(-6)\right)\right]+\left[0-\left(\frac{(-3)^{2}}{2}+3(-3)\right)\right]$
$=-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]$
$=9$