Solve each of the following systems of equations by the method of cross-multiplication :

GIVEN: 

$\frac{x}{a}+\frac{y}{b}=a+b$

$\frac{x}{a^{2}}+\frac{y}{b^{2}}=2$

To find: The solution of the systems of equation by the method of cross-multiplication:

Here we have the pair of simultaneous equation

$\frac{x}{a}+\frac{y}{b}-(a+b)=0$

$\frac{x}{a^{2}}+\frac{y}{b^{2}}-2=0$

By cross multiplication method we get

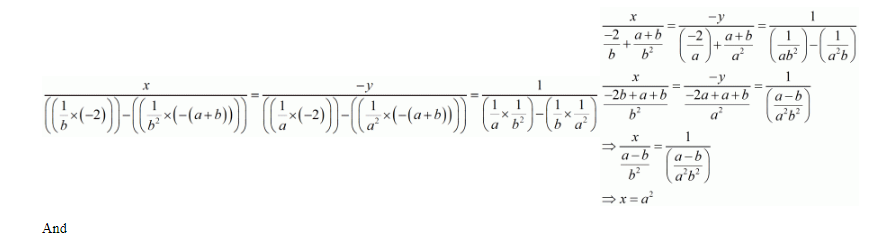
$\frac{-y}{\frac{-2 a+a+b}{a^{2}}}=\frac{1}{\left(\frac{a-b}{a^{2} b^{2}}\right)}$

$\frac{-y}{\frac{-2 a+a+b}{a^{2}}}=\frac{1}{\left(\frac{a-b}{a^{2} b^{2}}\right)}$

$\Rightarrow \frac{y}{\frac{a-b}{a^{2}}}=\frac{1}{\left(\frac{a-b}{a^{2} b^{2}}\right)}$

$\Rightarrow y=b^{2}$

Hence we get the value of $x=a^{2}$ and $y=b^{2}$