Solve each of the following systems of equations by the method of cross-multiplication :

GIVEN:

$\frac{x+y}{x y}=2$

$\frac{x-y}{x y}=6$

To find: The solution of the systems of equation by the method of cross-multiplication:

Here we have the pair of simultaneous equation

$\frac{x+y}{x y}=2$

$\frac{1}{x}+\frac{1}{y}=2$

$\frac{1}{x}+\frac{1}{3}-2=0$...(1)

$\frac{x-y}{x y}=6$

$\frac{1}{y}-\frac{1}{x}=6$

$\frac{1}{y}-\frac{1}{x}-6=0$ ...(2)

Let

$u=\frac{1}{x}$ and $\frac{1}{y}=v$

$u+v-2=0$...(3)

$-u+v-6=0$...$(4)$

By cross multiplication method we get

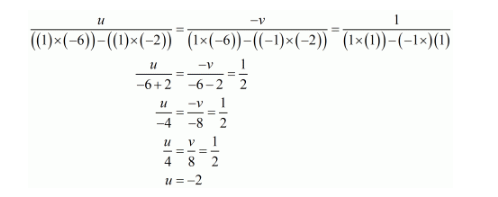
So $\frac{v}{8}=\frac{1}{2}$

$v=4$

We know that

$-2=\frac{1}{x}$ and $\frac{1}{y}=4$

$\Rightarrow x=-\frac{1}{2}$ and $y=\frac{1}{4}$

Hence we get the value of $x=-\frac{1}{2}$ and $y=\frac{1}{4}$