Solve each of the following systems of equations by the method of cross-multiplication :

GIVEN:

$a x+b y=a^{2}$

$b x+a y=b^{2}$

To find: The solution of the systems of equation by the method of cross-multiplication:

Here we have the pair of simultaneous equation

$a x+b y-a^{2}=0$

$b x+a y-b^{2}=0$

By cross multiplication method we get

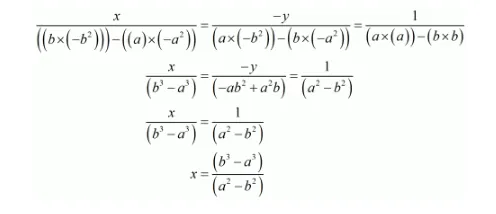
$x=\frac{(a-b)\left(a^{2}+a b+b^{2}\right)}{\left(a^{2}-b^{2}\right)}\left\{\sin c e\left(a^{3}-b^{3}\right)=(a-b)\left(a^{2}+a b+b^{2}\right)\right\}$

$x=\frac{\left(a^{2}+a b+b^{2}\right)}{(a+b)} \quad\left\{\right.$ since $\left.\left(a^{2}-b^{2}\right)=(a+b)(a-b)\right\}$

And

$\frac{-y}{\left(-a b^{2}+a^{2} b\right)}=\frac{1}{\left(a^{2}-b^{2}\right)}$

$y=\frac{\left(-a b^{2}+a^{2} b\right)}{\left(a^{2}-b^{2}\right)}$

$y=\frac{(-a b(a-b))}{\left(a^{2}-b^{2}\right)}$

$y=\frac{(-a b(a-b))}{(a-b)(a+b)}\left\{\right.$ since $\left.\left(a^{2}-b^{2}\right)=(a+b)(a-b)\right\}$

$y=\frac{-a b}{(a+b)}$

Hence we get the value of $x=\frac{\left(a^{2}+a b+b^{2}\right)}{(a+b)}$ and $y=\frac{-a b}{(a+b)}$