Solve for x:

To find: value of $x$

Given: $\cos \left(\sin ^{-1} x\right)=\frac{1}{9}$

LHS $=\cos \left(\sin ^{-1} x\right) \ldots$ (1)

Let $\sin \theta=x$

Therefore $\theta=\sin ^{-1} \times \ldots$ (2)

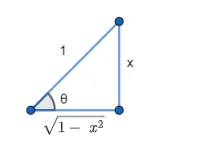
From the figure, $\cos \theta=\sqrt{1-x^{2}}$

$\Rightarrow \theta=\cos ^{-1} \sqrt{1-x^{2}} \ldots$ (3)

From (2) and (3),

$\sin ^{-1} x=\cos ^{-1} \sqrt{1-x^{2}} \ldots$ (4)

Substituting (4) in (1), we get

$\mathrm{LHS}=\cos \left(\cos ^{-1} \sqrt{1-\mathrm{x}^{2}}\right)$

$=\sqrt{1-\mathrm{x}^{2}}$

Therefore, $\sqrt{1-\mathrm{x}^{2}}=\frac{1}{9}$

Squaring and simplifying,

$\Rightarrow 81-81 x^{2}=1$

$\Rightarrow 81 x^{2}=80$

$\Rightarrow \mathrm{x}^{2}=\frac{80}{81}$

$\Rightarrow \mathrm{x}=\pm \frac{4 \sqrt{5}}{9}$

Therefore, $\mathrm{x}=\pm \frac{4 \sqrt{5}}{9}$ are the required values of $\mathrm{x}$.