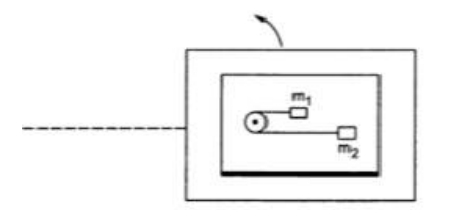
A table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius $\mathrm{R}$ (figure 7-E5). A smooth pulley of small radius is fastened to the table. Two masses $m$ and $2 m$ placed on the table are connected through a string going over the pulley. Initially the masses are held by a person with the strings along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
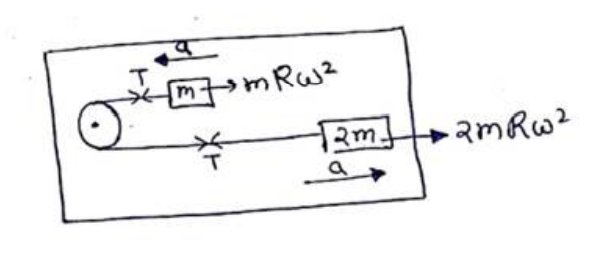
$2 m R \omega^{2}-T=2 m a$
$\mathrm{T}-\mathrm{mR} \mathrm{w}^{2}=\mathrm{ma}$
Adding both,
$m R \omega^{2}=3 m a$
$a=\frac{R w^{2}}{3}$
$\mathrm{T}-\mathrm{mR} \omega^{2}=\frac{\mathrm{m}\left(R w^{2}\right)}{3}$
$\mathrm{T}=\stackrel{\frac{4}{3}}{\mathrm{~m}} \mathrm{mR} \omega^{2}$