Two particles of masses $m_{1}$ and $m_{2}$ are joined by a light rigid rod of length $r$. The system rotates at an angular speed $\omega$ about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is $L=\mu r^{2} \omega$ where $\mu$ is the reduced mass of the system defined as
$\mu=\frac{m_{1} m_{2}}{m_{n}+m_{2}}$
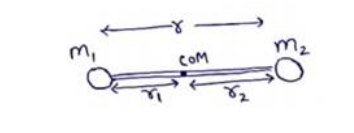
Distance of COM from $m_{1}$ will be $r_{1}=\frac{m_{2} r}{\left(m_{1}+m_{2}\right)}$ Distance of COM from $m_{2}$ will be $r_{2}=\frac{m_{1} r}{\left(m_{1}+m_{2}\right)}$
$\mathrm{L}=\mid \omega$
$\mathrm{L}=\left(m_{1} r_{1}^{2}+m_{2} r_{2}^{2}\right) \omega$
$\mathrm{L}=\left[m_{1}\left(\frac{m_{2} r}{\left(m_{1}+m_{2}\right)}\right)^{2}+m_{2}\left(\frac{m_{1} r}{\left(m_{1}+m_{2}\right)}\right)^{2}\right]$
$\mathrm{L}=\mu r^{2} \omega$ where $\mu=\frac{m_{1} m_{2}}{m_{1}+m_{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
