Question:
A uniform rod of length $L$ sets against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that the rod can make with the horizontal is $\theta$.
Solution:
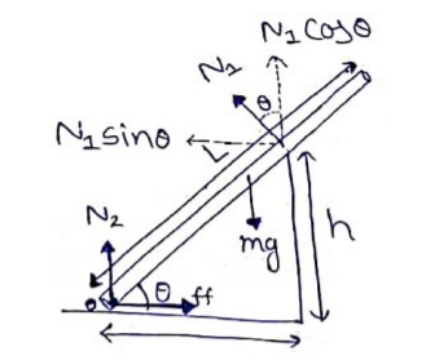
Translatory equilibrium
$N_{1} \cos \theta+N_{2}=m g g_{-(i)}$
$N_{1} \sin \theta=f f$-(ii)
Rotational Equilibrium about bottom
$N_{1}\left(\frac{\hbar}{\sin \theta}\right)=m g\left(\frac{L}{2} \cos \theta\right)$
$f f=\mu N_{2}$-(iv)
Solving (i),(ii),(iii) and (iv)
$\mu=\frac{L \cos ^{2} \theta \sin ^{2} \theta}{2 h-L \cos ^{2} \theta \sin ^{2} \theta}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
