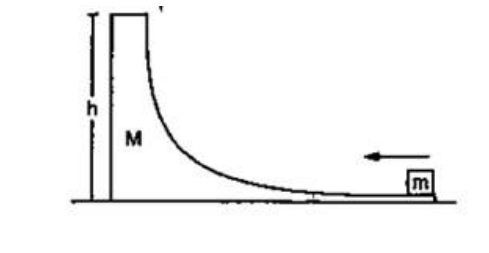
Figure shows a small body of mass $\mathrm{m}$ placed over a larger mass $\mathrm{M}$ whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the larger ones at a speed $v$ and the system is left to itself. Assume that all the surfaces are frictionless. (a) Find the speed of the larger block when the smaller block is sliding on the vertical part. (b) Find the speed of the smaller mass when it breaks off the larger mass at height $h$. (c) Find the maximum height (from the ground) that the smaller mass ascends. (d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.
(a) Use C.O.L.M
$m v=(M+m) v_{1}$
$v_{1}=\frac{m v}{M+m}$
(b) Use C.O.E.L
$\frac{1}{2} m v^{2}=\frac{1}{2} M v_{1}^{2}+\frac{1}{2} m v_{2}^{2}+m g h$
$\Longrightarrow v_{2}=\sqrt{\frac{\left(m^{2}+M m+m^{2}\right) v^{2}}{(M+m)^{2}}-2 g h}$
(c) $v_{y}^{2}=v_{2}^{2}-v_{1}^{2}$
$\{$ resultant velocity\}
$=\frac{M^{2}+M m+m^{2}-m^{2}}{(M+m)^{2}} v^{2}-2 g h$
$v_{y}^{2}=\frac{M v^{2}}{(M+m)}-2 g h$
Use C.O.E.L
$\frac{1}{2} m v_{y}^{2}=m g h_{1}$
$h_{1}=\frac{v_{y}^{2}}{2 g}$
Total height $=h_{1}+h$
$=\frac{v_{y}^{2}}{2 g}-\frac{v_{y}^{2}}{2 g}+\frac{M v^{2}}{(M+m) 2 g}$
$=\frac{M v^{3}}{(M+m) 2 g}$
(d) time for flight
$t_{1}=\frac{v_{y}}{a}$
Total time $=2 t_{1}=\frac{2 v_{y}}{g}=T$
$S=v_{1} T=\frac{m v}{M+m} \times T$
$=\frac{2 m v\left[M v^{2}-2(M+m) g h\right]^{\frac{1}{2}}}{(M+m)^{\frac{8}{2}} g}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
